statesoli.blogg.se - Piecewise defined functions

Due to this diversity, there is no " parent function" for piecewise defined functions. A piecewise function is a function in which more than one formula is used to define the output. Their "pieces" may be all linear, or a combination of functional forms (such as constant, linear, quadratic, cubic, square root, cube root, exponential, etc.). It means it has different definitions depending upon the value of the input. Piecewise defined functions can take on a variety of forms. A piecewise function is a function with multiple pieces of curves in its graph. Because these graphs tend to look like "pieces" glued together to form a graph, they are referred to as " piecewise" functions ( piecewise defined functions), or " split-definition" functions.Ī piecewise defined function is a function defined by at least two equations ("pieces"), each of which applies to a different part of the domain. These graphs may be continuous, or they may contain "breaks". Category Archives: 3.4 Library of Functions Piecewise-defined Functions Graphing Basic Functions: The Absolute Value Function Graphing Basic.

There are also graphs that are defined by "different equations" over different sections of the graphs. We have also seen the " discrete" functions which are comprised of separate unconnected "points". With beautiful typesetting (including all the words ‘ if ’ lined up vertically), this author prefers the simplest formatting, with no extra punctuation.We have seen many graphs that are expressed as single equations and are continuous over a domain of the Real numbers. Such a function is said to be defined piecewise. The hollow dot at $\,\color\quad -1 \le x < 1\cr A function may be defined by different formulas on different portions of the x x -axis.

There is a rule that applies to the left of $\,x\,$.

This is an actual point on the graph of the function it is an (input,output) pair. This produces the solid (filled-in) dot, with coordinates $\,\bigl(x,f(x)\bigr)\,$.

There is a rule that applies at $\,x\,$.

In this example, three rules are needed to fully understand what happens at and near $\,x\,$: A function may employ different formulas on different parts of its domain. You may need up to three ‘dots’ to fully understand what's happening at a place where rules are changing. Graphing a Piecewise-Defined Function When a graph is ‘pieced together’ using different rules, as in a piecewise-defined function, Just use the ‘collapse the graph into the $\,y\,$-axis’ method, as described in this earlier lesson.

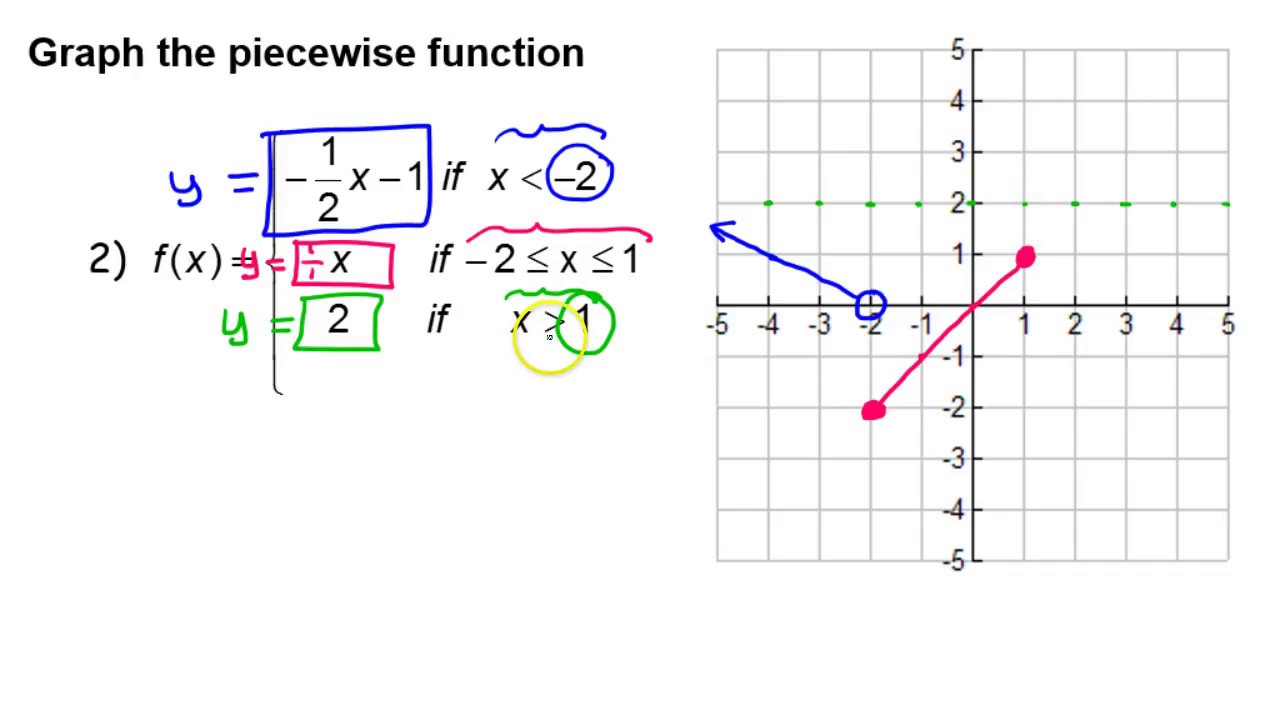
Once you have a graph, though, the range is easy to obtain: Reading a Piecewise-Defined Function AloudĪloud, it is typically read from left-to-right and top-to-bottom.īy the way, the range of $\,f\,$ is nowhere near as easy to get from the formula. The first step in evaluating a piecewise. for inputs in the interval $\,[2,\infty)\,$ the quadratic function $\,x^2\,$ is used for the outputs A piecewise fucntion exists when a function is defined by two or more different functions throughout its domain.for inputs in the interval $\,[1,2)\,$ the constant function $\,5\,$ is used for the outputs.for inputs in the interval $\,[-1,1)\,$ the linear function $\,-x+3\,$ is used for the outputs.Finding Function Values for a Piecewise-Defined Function This function $\,f\,$ uses three rules (one for each row) that is, it has three ‘pieces’ (hence the name piecewise-defined function):